Need to Know: Higher-Order Aberrations and Polynomials

Aberrations of the eye can be chromatic or monochromatic. Chromatic aberrations are caused by light dispersing into its component wavelengths, with different wavelengths focused at slightly different points. Thick lenses and materials with low Abbe value have higher dispersion and can decrease image quality—which is important for optical design and material selection in applications such as intraocular lenses, operating microscopes, and cameras.

Monochromatic aberration, on the other hand, is what we ophthalmologists often must deal with in the clinic while seeing patients with different corneal and lenticular pathologies. Defocus and astigmatism contribute to 85% of monochromatic aberrations; these are referred to as lower-order aberrations (LOA). These are typically fully corrected with spherocylindrical lenses and do not result in degradation of vision.

The other 15% constitute higher-order aberrations (HOA), which lead to decreased vision that is not fully correctable by spherocylindrical lenses. They result in an irregular wavefront rather than plane (parallel rays) or spherical (converging or diverging rays coming to a point of focus) wavefronts. HOAs are primarily due to corneal pathology, though other conditions such as a crystalline lens or the IOL may also be responsible.

Wave aberration

Total ocular aberrations are composed of corneal aberrations and internal aberrations. This quantifies the overall magnitude of wavefront deviations from an ideal wavefront, plotted in microns on the exit pupil and dependent on pupil size. Root mean square (RMS) wavefront error (WE) refers to the square root of the mean of these squared deviations. This is preferred over a simple mean to avoid aberrations of opposite signage cancelling each other out. The RMS thus helps estimate the average magnitude, independent of sign.

Mean absolute deviation (MAD) takes the absolute value of each deviation before averaging. However, it gives equal weight to all deviations irrespective of size. On the other hand, the RMS squaring process gives more weight to larger deviations to make it a better measure of the optical performance and error in a system. RMS is thus generally higher than MAD.

Standard deviation (SD) of WE is generally used for statistical analysis to reveal the variation of values around the mean. In contrast, RMS measures deviation from the reference plane and estimates the total wavefront quality. Therefore, it is the RMS and not MAD or SD of WE used to evaluate human eyes.

Wavefront representation

The American National Standards Institute (ANSI) representation of WE uses the two-dimensional polar coordinate system: (a) r, the radial coordinate (normalised pupil radius: zero at the centre, one at the edge), and (b) θ/theta, the azimuthal angle (angle in radians around the pupil centre). The mean of the wavefront is assigned zero level (green) and separated into two halves, the advanced from the delayed phases. The WE refers to the optical path difference from the reference surface (green level).

The wavefront can be represented by the Zernike polynomial system, the Fourier, or the Gatinel–Malet systems.

Zernike polynomials

The shape of the wavefront appears as a sum of Zernike polynomials, each describing a certain deformation. The weight of each Zernike mode is determined by the RMS coefficient of a Zernike wavefront decomposition. The magnitude of the coefficient of each mode indicates its relative contribution to total WE. However, the largest Zernike coefficient need not affect vision the most. Different Zernike modes affect vision to different extents. Zernike modes may also interact with each other, increasing or decreasing the effect on image quality.

The RMS value of the Zernike modes is dependent on pupil size, with larger pupil size exposing higher RMS values. The amplitude of variation with pupil diameter is exponential—with larger variation seen with higher radial degrees when the pupil diameter increases.

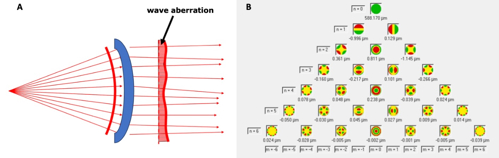
Zernike polynomials are represented on the Zernike pyramid, which has infinite modes. The first 6 orders contain 28 modes, each mode having a mean of 0. In the polynomial domain, there are multiple modes—each in a different dimension, represented by its unit vector, and orthogonal to all others. The WE in this multidimensional space is represented by a vector, which is the sum of the weighted unit vectors or the Zernike modes.

Additionally, the polynomials may be represented by a single index system (Noll’s index), which assigns a single number (j) to each Zernike polynomial in a standardised sequence and is useful for plots, charts, and software analysis. They may also be represented by the double index Optical Society of America (OSA) and Vision Science and Its Applications (VSIA) system which uses two indices: radial order (n) and azimuthal order (m). Each Zernike mode has a numerator (m), a continuous function that repeats every 2π radians and gives the number of affected meridia. The ‘m’ indicates the type of function (cosine or sine component) and a denominator (n, a radial function proportional and corresponding to the order of polynomials). This is often used in scientific publications and clinical ophthalmology.

The mathematical expression for each Zernike mode (Zn_m) consists of: (a) a normalising constant that converts the RMS of each function to a value of 1 on a pupil radius of 1; (b) a polynomial function in r composed of n (radial degree/order, which is always positive), m (azimuthal/angular frequency, which may be positive or negative), and k [0≤k≤(n-m)/2 or 0≤k≤(n+m)/2]; and (c) a trigonometric function in t for rotationally asymmetric azimuthals. Rotationally symmetrical azimuthals have no angular dependency as m=0. The central column of the Zernike pyramid contains these rotationally symmetrical modes. Defocus and spherical aberration are examples of m=0.

Fourier transform

Fourier transform uses trigonometry-based decomposition, unlike the polynomial-based expansion in Zernike. The measured WE is subjected to a Fourier transform, which decomposes the wavefront into sinusoidal components (sine and cosine waves)—i.e., into its constituent spatial frequencies (frequency domain representation). Low spatial frequencies show the overall shape and are constituted by large refractive errors such as myopia and hyperopia. High spatial frequencies represent finer details and are constituted by HOAs. Fourier works well for rotationally symmetrical WE and describing corneal shape abnormalities.

Unlike Zernike, which is defined over a unit circle, Fourier is defined over all the space or periodic domains. It is not limited to a circular domain and can be adapted to irregular pupil shapes. It works in both spatial (Fourier optics) and temporal (signal analysis) domains. It is thus effective for keratoconus detection and contact lens fitting, image processing, diffraction analysis, and filtering while Zernike polynomials are useful for customised refractive surgery and adaptive optics.

Gatinel–Malet polynomials

Some higher-order Zernike modes are impure and contaminated by lower-order modes. The RMS of these higher-order modes also reflects lower radial degrees of identical azimuthal frequency. For example, spherical aberration and secondary astigmatism also contain lower-order defocus and astigmatism, whereas coma contains tilt. These contaminations bring unnecessary central distortions into the HOAs, which then require an offset by introducing unwanted LOAs such as defocus or tilt.

Thus, Zernike polynomials have the disadvantage of failing to completely separate LOA from HOA and even decreasing the values of certain HOAs. This property makes it difficult to predict the sphero-cylindrical correction, astigmatism orientation, point spread function, and retinal image quality from the wavefront. It can also interfere with contrast evaluation and accurate customisation of refractive surgery.

LOAs mostly affect the centre of the wavefront while most HOAs are flat in the centre, meaning HOAs degrade acuity with larger pupil diameters. In the Zernike expansion, LOAs are calculated with quadratic polynomial functions (highest exponent value of two) while HOAs are calculated with polynomial functions that are cubic or higher. However, many HOA polynomials are contaminated by the presence of significant LOAs. This creates artefactual central distortions in the HOAs, which are more significant towards the centre of the Zernike pyramid (e.g., coma, spherical aberration, secondary astigmatism). These central distortions are then cancelled in the Zernike expansion by artefactually creating LOAs.

Positive spherical aberration contains hidden hyperopia, negative spherical aberration contains hidden myopia, coma contains tilt, and secondary astigmatism contains some lower astigmatism. Dr Damien Gatinel and colleagues therefore defined a new polynomial function to separate the two aberration types. Some Zernike modes are retained on the pyramid sides since these are pure. However, to the centre, the conventional Zernike modes are replaced with modes that have a flat centre, thus interfering less with paraxial refraction. Gatinel–Malet’s LD/HD decomposition gives the added advantage of being able to study the actual influence of the uncontaminated HOAs on vision.

This is the first in a multipart tutorial on higher-order aberrations.

Dr Soosan Jacob is Director and Chief of Dr Agarwal’s Refractive and Cornea Foundation at Dr Agarwal’s Eye Hospital, Chennai, India, and can be reached at dr_soosanj@hotmail.com.